田口玄一先生の考案された品質工学を活用すると、技術評価、機能性評価の時間が劇的に短縮できます。
それだけでは無く、懸念される様なことや、コストダウン出来そうなことも試す余裕が生まれます。
中小企業の技術開発の現場を見ていると、初めての試作品がある程度の性能を満たしていると、すぐに製品化を目指して、量産化設計に入ることが少なくありません。
しかし、それは大きなリスクを含んでいます。
1.企業経営と新製品開発
製造業では,社会に製品を供給して,その対価として得た収入を売上に計上している.しかし,社会に提供された製品は永久に売れ続ける訳ではなく,ある製品寿命を持っているのである.
今まで無かったような新しい機能を持った製品のライフサイクルは,横に時間軸を設け,縦に売上高などを使うと次のような関係になる.(E.M.Rogers 1966)
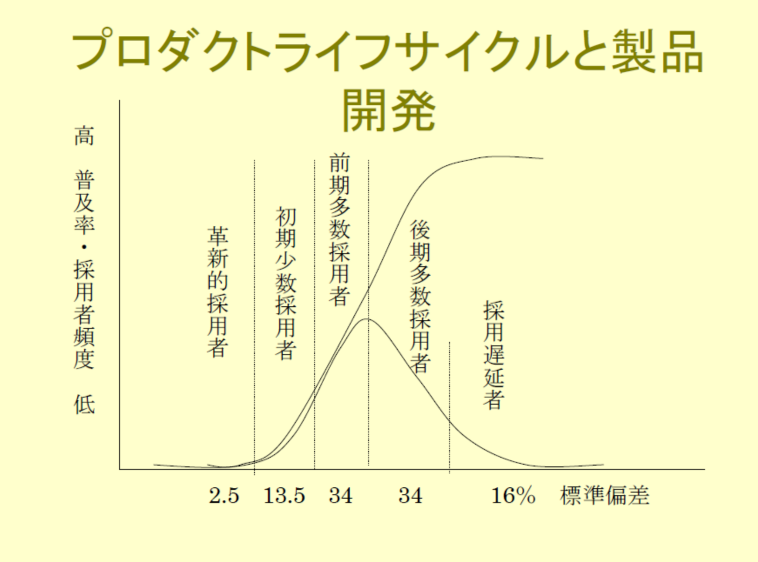
①革新的採用者(イノベーター)リスクを厭わず,新しい技術を試すことに熱心
②初期少数採用者(アーリーアダプター)価値観の先行モデルとして仲間から尊敬される
③前期多数採用者(アーリーマジョリティー)
④後期多数採用者(レイトマジョリティー)
⑤採用遅延者(ラガーズ)
ただし,競合会社が存在するために,上記の製品ライフサイクルの曲線における後半のタイムスケールが急速に短縮されて頻度曲線が急降下する事も少なくない.上記のグラフはあくまで理論であって,現実では曲線はゆがんでしまうのである.また,企業の継続性を考えると,会社全体の頻度曲線の総和は右上がりでなくてはいけないのである.すなわち,製品ライフサイクルの頻度曲線が右下がりになってくる頃に,次期新製品の投入をおこなって該当事業領域で既存製品と新製品で合計された頻度曲線が右下がりにならないように操作してゆくことが必要である.頻度曲線は,ほぼ売上高に比例しているので,企業の経営目標に,新製品開発が非常に深く関わっていることがわかる.
これらの考え方を総合して,企業では商品ミックスというものを計画している.企業の対象とする市場をある程度細分化しながら,それぞれの市場に対し,投入した製品のライフサイクルが終わる前に,新製品を投入し続けていくことが重要である.
2.製品開発のタイプ
新製品は現製品の需要が低迷する頃には,すでに投入されなければならない.新製品開発は瞬間的に完成するわけではないので,新製品開発に必要な期間だけ以前から着手しなければならない.すなわち,計画したタイミングで,計画した仕様の製品を市場に投入できるかどうかが,企業の業績に大きく寄与するのである.それは,製品開発のプロセスをコントロールするということとほぼ等価である.以下の図はプロダクトミックスの例であるが,市場分野ごとに製品の投入計画を立案してある.このスケジュール通りに,製品の後継機種を開発して投入していくのである.製品の投入スケジュールは,それぞれの製品ライフサイクルが異なるので,それに合わせてインターバルが設定されているが,当然の事ながら競合相手の製品投入時期を予測して効果的な時期に,効果的な仕様の製品を投入することが大切である.
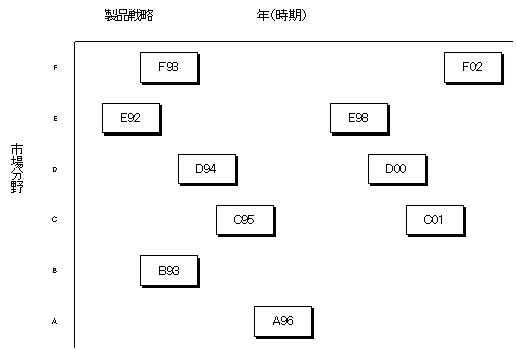
必然的に,製品開発は決められた時期までに,競合製品や自社の現有製品に対して,価格や仕様において十分に顧客満足を満たすような製品を,目標とされる時期までに開発を秘密裏のうちに完了することが大切である.特に競合会社が市場に新製品を投入する直前に,価格・品質・機能全てにおいて上回った新製品を投入することが,競合製品に対して最もダメージを与えることができるのである.
また,予想外の技術革新や,市場の変化などによって,開発の中止や計画の前倒し,凍結などもまれには発生する.競合会社が予想外の機能や,コストを実現して新製品を市場投入してきたりすると,それに応じて急遽開発中の製品の目標を変更したりすることもある.
製品開発の概略のプロセスは大きく4段階(フェーズ)になる.仕様決定の段階から,設計,生産準備,生産へと流れてくるのである.その中で,製品化段階を通じて日の目を浴びる技術は,ごく一部で,大半は技術の川を漂っているという状況である.
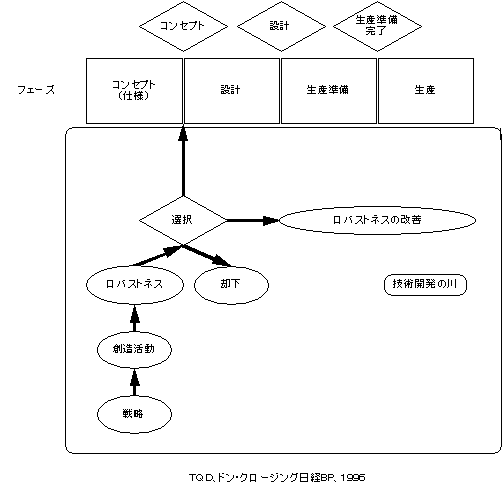
この,技術の川から要素技術をすくい上げて,生産までのラインに乗せることが,技術部門の役割である.
3.製品開発の過程とその内容
4.製品開発の概略プロセス
現実の製品開発では,製品企画の以降の設計段階でもう少し詳細な手順を踏む.右図に有るように,製品設計の段階で,いくつかの目的を持った段階を経ながら,完成度を上げていくのである.もっとも基本的な技術を評価するために経るステージが,ベンチモデルである.ここで候補技術の技術選択を中心に行う.なるべく複数の候補技術を並列に並べて技術選択をすることが好ましいが,現実的にはなかなかそれができない.多くの場合は,サブシステム毎に独立してサブシステムテストで終わってしまうことが多い.本来の目的としては,採用しようとしている技術のロバストネス(堅牢性)を評価して,安定したシステムを選択できるとよい.この段階での技術選択が,最終的な製品の市場での評価や,製品のライフサイクルを決めることにもなり,収益性にも大きな影響を持っているので,慎重に判断すべきである.次のステージはフィージビリティーモデルである.ここでは,市場に出すような汎用性を持っているのかという事を評価しながら,技術レベルを上げていくフェーズである.量産性を持たせるには,一流の部品で構成しては実現できない.実現しようとする製品を構成する部品が,一般的な方法で調達できそうなのかということを評価する.次のステージがエンジニアリングモデルである.ここでは,性能目標のクリアと原価目標のクリアが重要な事になってくる.VE活動の中心はこのステージで実施される.その次のステージが,プロとモデルによる評価である.極力量産品を作るときと同じ製造方法で製造し,量産への確認をするためのモデルである.これをクリアすれば,量産試作モデルを経て製造販売といった手順に進む.
前項で示したフローは,省略無しの全工程を示しているが,すべての製品開発がこの様な工程を経ているわけではない.ベンチモデルは新規の技術分野に進出する場合には必要となる部分であるが,後継機種や類似の機種を開発する場合などは,この部分をとばして次のフィージビリティーモデルやエンジニアリングモデルから開始することが多い.

5.フェーズ内での定常プロセス
また,各々のフェーズの中で,右図のような詳細なプロセスを踏んでいるのが現実である.

まず初めに構想検討を行う,次に構想図を作成するわけであるが,実際は,採用しようとしている技術(仮説)が果たして使用可能かどうかを確認する必要があるために予備実験を行うことが多い.この予備実験の結果重大な欠陥を発見したり,奇抜なアイデアを思いついたりする.そして,構想図が仕上がってくると設計審査といってプロジェクトメンバーが全員集合して,それぞれの仮説を披露し合い全体のシステムとして矛盾がないかどうかを確認する.
矛盾がなければ部品図の制作へとはいる.部品図が完成してくると,また設計審査を行い構想と部品の矛盾はないか?部品どうしの矛盾・干渉は無いかを確認する.そして,矛盾がないことがわかると組立図を作成する.組立図に関しても設計審査を行う.その時点で審査をパスすると試作発注になる.その後,試作組立が行われ,部品の干渉や不具合から部品の修正が必要になれば,その場で部品図を変更していく.これをデバッグと呼んでいる.デバッグが完了すると,設計通りの機能が出ているか?の評価テストを行いフェーズ移行の審査を受けることになる.ここで合格していれば,次のフェーズに移行して,前モデルで積み残した問題点などをクリアするための構想に入る.このサイクルをフェーズ毎に繰り返すのである.
6.品質改善活動
製品開発活動の中で品質改善活動は,必要とされる重要な活動の一つである.試作してみたモデルの品質が目標に達しないことは当然である.現状の品質レベルを目標に到達できるように向上させるのが技術部門の役割である.この活動の根幹となる手順が,試作品制作とその評価である.試作品を制作する過程では,仮説を立案してその仮説を検証するために試作品を制作してみるわけである.仮説を精密に立てられるかどうかが重要となる.そのために品質管理活動の手法(QC7つ道具,新QC7つ道具)はひと通り知っておく必要がある.また,仮説を立案するときは,FTA,FMEAなどを作って整理をする必要もある.FTAを右図に示す.故障する要因を推定して,そのパラメータの中心値と実験で確認するパラメータの範囲を推定しておくのである.これらは,このあとの製品開発が進む段階で,次第に精密になっていき,市場での整備マニュアルに流用されていく.また,新人の設計者の教育などにも活用される事になる.
また故障モードの影響分析も次のような例にあるように,設計段階の仮説立案の段階で想定しておくことが大切である.これもその後の用途として,サービスマニュアルや,ノウハウの伝承などに使えるので精密に作成し,仕上げていくようにする.

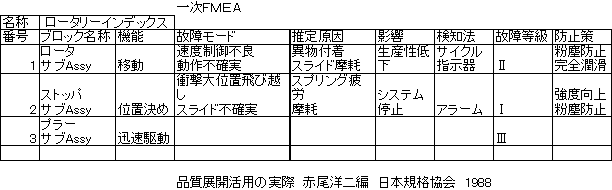
試作品を組み立てていく段階で,組立性をチェックしながら,次のモデルへの修正を検討していくのであるが,現実には,この時点で部品の干渉が発生することが良くある.特急で修正や追加工しながら組み立てていくのである.
試作品ができあがると,まず必要となるのは,機能性評価実験である.設計者がねらったような機能を発揮できるかどうかを検証する.このとき,目標値を達成するためにいくつものパラメータを変更しながら実験を行うのである.外乱としてのストレス条件も積極的に取り入れて評価する.モデル間較差に関しても,安易に考えていると重要な要素を見逃すことにもなる.この時のパラメータテストに使う部品は,あらかじめ試作機の設計をする前に図面を作成しておく必要がある.特に重要なパラメータは実験間で設定変更がやりやすいように設計しておかないと,実験の時間が長くなる.また,パラメータ間の交互作用も問題となることが多いので,実験計画法(田口メソッド)などを活用して最小限の実験回数で最適パラメータの解を求めるようにする.
信頼性テストでは,統計的な知識が必要となる.とくに量産品を開発するとなると,市場に出したときの故障率を予測しなければメンテナンス部品の用意や,サービス体制の整備などが準備できない.この故障率の推定に関しては,サンプル数の決定や,信頼性確認実験の規模などにより決定される.
また,これらをシステム的に捉えた品質機能展開(QFD)という体系も考慮しながら品質と機能・部品・コストなどのバランスをとっていくことが重要である.
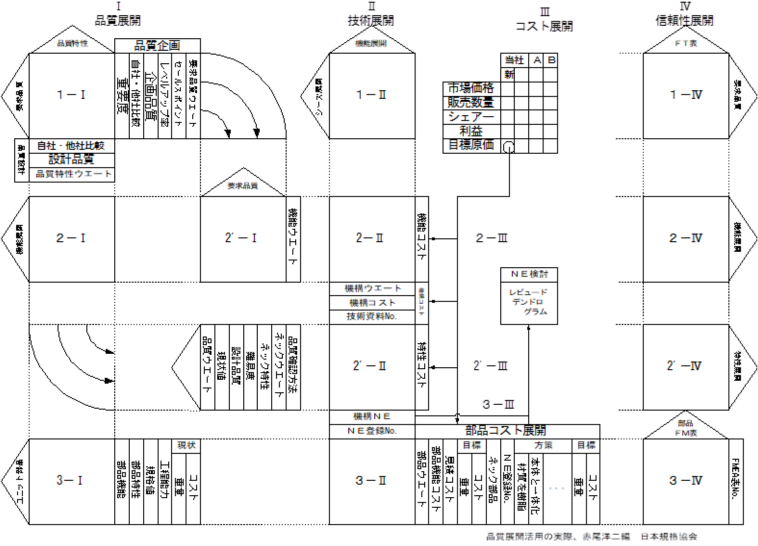
7.品質工学の考え方
従来の技術開発の方法は、次の様な3種類のアプローチがされていることが多いのです。
A.目標とする製品を試作し、評価実験により出てきた不具合に対して、トライアンドエラーを繰り返して製品の品質を向上させる。
B.品質不良となる要因を管理抑制する。(温湿度の管理、使用する部品・材料の公差を厳しくする、商品の使用条件の制限)
C.出力の変動を補償装置により補償する(温度補償、フィードバック制御)
これらの取り組みは一般的だが、次の様な欠点をもっています。Aの場合の欠点は、技術者はいつも品質問題に追われて残業休出に明け暮れている。そればかりか、発売日になっても問題が解決出来ずに、納期遅れになってしまうこともあります。Bの欠点は、温湿度の管理にエネルギーコストがかかることや、部品・材料の公差を小さくすることで、原価が高くなること、商品の使用制限をしたりすれば、対象市場を小さくすることになります。Cの欠点は補償装置のコストが余計にかかることや、補償装置の故障による故障率のアップにつながるのです。
これらの欠点を無くするためには、研究開発の手法そのものを見直さなければならなりません。まずは、システムの安定化を得るために、ばらつきが少なくなるパラメータの組み合わせを見つけることです。
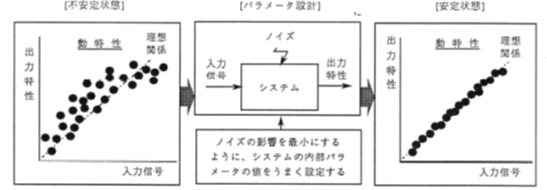
品質工学では、選択しようとする技術そのものの評価をSN比という尺度で評価することにより、システムの安定度を定量的に評価することを提案しています。またいくつもののパラメータの最適な組み合わせの中から最適な組み合わせを見いだすために多元配置の実験を行うと膨大な時間とコストを要することになります。品質工学では実験計画法として考案された直交表を活用することにより、劇的にパラメータ実験の回数を減少させることが出来るのです。故田口玄一氏は、研究開発者の残業時間を減らすために、この手法を開発したと語っていました。
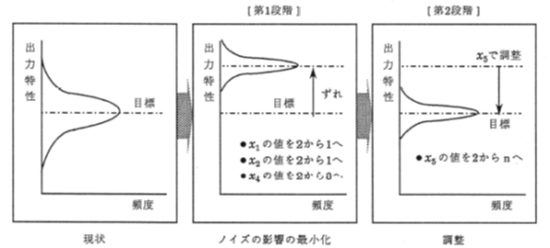
また、パラメータのシステムへの寄与の内ばらつきに寄与する因子(SN)比と、出力の大きさに寄与する因子(感度)に分解することにより、目標出力に近い状態で最もばらつきが小さいパラメータの組み合わせを選択することが可能になるのです。この特徴を利用して2段階設計を提案しています。
まず初めに、バラツキを小さくするパラメータの組み合わせを選択することが第一段階です。第二段階で、バラツキを大きくせずに出力だけを大きくするパラメータを調整して目標値に近づけます。これらのパラメータの特徴を短時間で把握するために、実験計画法とSN比が重要になります。
バラツキとそれが与える社会への損失の関係を定義した損失関数についても品質工学の特徴です。安全係数の考え方や、検査のサンプリングなども、損失関数で計算して決定することで、最適な検査手法の選択が出来ます。
品質工学を理解するためには、多少の統計的知識が必要ですが、それは比較的簡単です。取っつきにくい面も有りますが、全体像を理解することができれば、全く当たり前のことをしていることに気がつきます。
8.品質の考え方
工場で生産された製品は,得意先で品質トラブルを起こしたりして,クレームにつながったりしている.これは,顧客の要求する機能に対して製品の品質が十分満たされていないということである.
大砲で砲弾を発射させて,目標とする対象物に命中させる事例で考えてみる.まず目標に対して照準を合わせて発射するが,現実にはなかなか命中しない.1発目の発射により着弾した位置を確認して,2発目を発射する場合は,1発目のずれ量を勘案して方向を修正してから発射するわけだが,また命中しないことが多い.今度は全く条件を固定して砲弾を発射させたとしても,寸分違わずに同じ位置に着弾することは無い.このばらつきは,砲弾が飛行してゆく方向の風が影響していたり,火薬の量や,火薬の配合比がばらついていたりすることが影響するわけである.砲弾に関しても,その外径や,テーパーの精度や,表面荒さなど全く同じ条件を用意することは出来ない.
目標をはずす要因としては,大きく区分すると二つの要因に分けられる.一つ目は,大砲の向きが目標からそれていること.二つ目は,同じ条件で打っても散乱してしまうばらつきである.
同じ現象が生産現場でも発生しているのである.量産の生産条件を設定して,いざ量産に入っても,生産される製品がばらついてしまって,不良品が発生してしまうことがある.管理しようと思って管理図を書いてみると中心値がシフトしてしまっている場合とばらつきの範囲が広がってしまっている場合に区分できる訳である.中心値がシフトしてしまって不良率が上昇してしまっている場合は,中心値を目標値に修正してやればいいので,比較的簡単に目標値の修正が出来る.他方,中心値は目標値に合っているのに,ばらつきが大きい場合は,ばらつきを小さくすることによってのみ改善できる.ばらつきを小さくすることが出来なければ,工程のどこかに検査工程を追加して,不良品を取り除くか?手直しして,良品に修正して次工程に送ればいいわけである.しかし,それは全てコストがかかる事になる.検査コストに加えて,不良品を廃却するコスト又は手直しするコストがかかるのである.
従って,製品の生産状況がどの様になっているかに関して,中心値が目標に対してずれているのか,それともばらつきが大きいのかを区分することにより対策が異なってくるのである.よって,なるべく早くどちらの効果が大きいのかを見極めることによって素早い対策が可能となるのである.
8.1品質の定義
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
品質工学では,品物の品質を次のように定義している.
「品質とは,品物が出荷後,社会に与える損害である.ただし,機能そのものによる損失はのぞく.」
品質の定義に対して,価値で評価すべきであるという主張があるが,品物の価値に関しては,一人一人の人間で異なるのである.一人一人異なる価値の評価問題は企業として重要な問題であるが,マーケティングの対象であり,工学や技術の対象にならない.
品質の定義に対するもう一つの問題は,損失の内容についてである.品質の定義としての損失を,次の二つに限定したいのである.
①機能のばらつきによる損失
②弊害項目(使用コストも含む)による損失
価格は,初めに社会に与える損失である.従って,同じ機能をもたらす製品の価格が異なれば,高価な方が品質が悪いと言うことである.また,たばこや酒の様に,機能そのものが,社会に損失を与えるものはその損失を品質に結びつけない.

8.2設計者の役割
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
設計部門は,企画で決められた機能を持つ製品を,企画で要求されたコスト(販売価格の数分の1)制限のもとで,納期までに開発する重要な任務を持っている.そのために用いられる手段が次の4つのステップである.
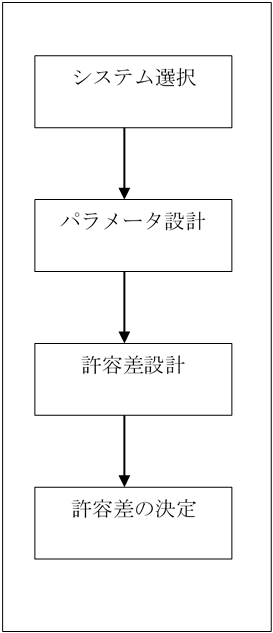
①システム選択
同じ機能を持つさまざまなシステムが考えられる.無数に近いシステムから,目的に合致する物を選ぶことをシステム選択という.開発部門に余力が有る場合には,複数のシステムを並行して開発することもある.
機能しなかった時に安全設計をするかどうかを考慮するのもシステム選択の仲間である.
たとえば,現在コンピュータ出力に多数使われている,プリンターでも,ドットマトリクスプリンター,インクジェットプリンターと,レーザープリンターが使われているが,それぞれの中でも,異なるシステム選択がされている.
②パラメータ設計
選んだシステムの中の設計定数(システムパラメータ)を品質とコストの両方を改善するために選択する行為である.機能をばらつかせる誤差原因の影響を減衰させる方法で,昔から非線形の利用,ノイズとの交互作用の利用といわれている.パラメータ設計については,いままで解析的方法,非線形計画法,機能範囲拡大法(OperatingWindow Method)などが技術の世界で用いられてきたが,品質工学はもっと能率の良い方法を提供する.
③許容差設計
パラメータ設計後,様々なシステム要素である部品,材料などのグレードの選択行為で,品質とコストのトレードオフの方法である.機能限界と,機能しなかったときの損失から,近似的な損失関数をもとめ,それを利用する方法である.
④許容差(公差)の決定
許容差設計で決まった部品,材料に対して,仕様書や図面に書き入れる契約上の許容差(公差)の決め方を述べる.
システム選択に対する最終評価は,許容差設計を終了して初めて可能である.
8.3構成段階と開発
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
設計には製品によって異なるが,次のような構成段階がある.
①トータルシステム
②サブシステム
③ユニットや部品
④素子や個片の開発
⑤素材の開発
これらのどの段階でも,前述の4つのステップがある.それぞれの中で,システムを選択して,その設計をするステップには安全設計も含まれており,もっとも重要である.
システムの選択設計者は,理想機能の定義と,理想機能からのずれに対する許容差を決定する重要な仕事がある.機能しなかったときのトラブルが生命に関係したり,社会上大きな損失を与えるときには,安全設計,冗長設計を考えることが大切である.
サブシステムの開発も同時に進める場合は,トータルシステムの設計者は,いわゆる機能はエネルギーの変換であるという認識のもとに,できる限りサブシステムの開発研究と並行して行うことが大切である.
8.4機能品質と企業活動
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
品質の中でわかりにくいのは,環境,劣化,品物間の差による機能のばらつき,すなわち製造段階のばらつきと出荷後の使用中の信頼性に対する対策である.機能品質に対する企業の活動を要約すれば,下表の様になる.
部門雑音の種類外部ノイズ
(環境)内部ノイズ
(劣化)品物間の
ばらつき
技術部門開発・設計システムの選択◎◎◎
パラメータ設計◎◎◎
許容差設計○◎◎
生産技術システムの選択××◎
パラメータ設計××◎
許容差設計××◎
ライン部門製造オンライン工程管理××◎
オンライン製品管理××◎
営業アフターサービス×△△
◎:対策可能 △:予防保全の意味としては可能
○:対策可能だができるだけ避ける ×:不可能
機能のばらつきの原因は,次の3種である.
①外部雑音(環境の差) 同じ製品が有る条件では機能するが,高温,高湿などの環境では機能しないときに,環境によるばらつきがあるという.
②内部雑音(劣化) 同じ製品が初期には機能するが,何年後かに機能しなくなるとき,劣化によるばらつきという
③品物間のばらつき 同じ仕様の製品のある物は正しく機能するが,中には機能しない物があるとき,品物間にばらつきがあるという.
これらのばらつき原因をノイズと呼ぶ.ノイズに強い製品の設計をするのが,製品の安定性設計である.
QC7つ道具にある,特性要因図を使って原因究明するとなると,無限の時間が必要になってくる場合がある.原因究明に時間をかけすぎては非効率である.任意に選択したノイズに対して安定的なシステムは,それ以外のノイズに対しても安定である確率が高い.システムを選択する場合には,システムの安定度を評価尺度として検討することが好ましい.システムの安定度が高いことが,社会への損害を少なくすることにつながるからである.しかし,システムの安定度が高くても,そのシステムのコストが高くては,社会への損害が大きいことになる.このシステムの安定度と,社会への損害の関係は,損失関数として次節で示す.
良いシステムの選択とパラメータ設計が全ノイズに対する対策として重要であるが,システム選択は,技術的予想で行われるので,正しい判断は困難である.むしろ,選んだシステムでどこまで機能の安定性が良くなるのかのパラメータ設計を能率良く実行することが,システム選択の良否の最終判断に役立つのである.
9.2乗和とその分解
ある製品の目標値からの差をy1,y2,・・・yn とすると
(9.1)
・
・
・

(9.2)
目標値からの差yiは,偏り と偏りからの偏差 に分けられる.偏りからの偏差は個体差とも言う.ばらつきの総量を全変動(全2乗和)といい(9.3)式で示す.
(9.3)
9.1式の右辺の第1項は,偏りであるからその2乗の合計は偏りの大きさの総量である.取り上げているデータの平均の大きさであるから一般平均といい次式で示す.
(9.4)
次に9.1式の右辺の第2項の2乗の合計は,個々の値と平均的な偏りとの差,すなわち個体差の2乗和で,誤差変動または個体差変動といい次式で示す.
(9.5)
全2乗和の平均値を平均2乗誤差といい次のように表す.
(9.6)
誤差変動を(n-1)で割った値を誤差分散とよび
(9.7)
誤差分散の平方根が標準偏差sである.
(9.8)
10.損失関数と許容差設計
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
10.1特性値
品質評価のための計量特性は,大きく分けて静特性と,動特性に分かれる.動特性とは,出力をその時々で入力信号に応じて,いろいろ変化させたい物をいう.静特性とは,出力をいかなる条件でも一定にしたい物をいう.
静特性はさらに次のように分けられる
①望小特性:非負で小さいほど良い特性(公害となるような,騒音,雑音など)
②望大特性:非負で大きいほど良い特性(材料の強度など)
③望目特性:ある有限の目標値があって,目標値より小さくても大きくてもまずい特性
④百分率特性:熱効率のように0から100%までの値しかとらない特性
動特性
センサーや計測器の精度,工作機械の性能,乗り物の性能,通信システムの性能など目標値が必要に応じていろいろに変化する特性である.多くの場合,ある条件での誤差範囲やSN比で規格を与えることができる.
10.2損失関数
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
品質を合理的に評価するために以下のような損失関数を考える.
損失関数を簡単に表現すると,目標値通りの機能を実現すれば,社会に与える損失はゼロであるが,目標値から離れるに従って,損失が大きくなるという考え方である.
目標値からのずれ量を金銭的な表現に結びつけたことによって,候補システムを比較検討する場合の評価尺度がはっきりし,トレードオフの考え方も明確に導入できる.
以下に,論理的な説明を示す.
望目特性yの目標値をmとする.目標値mからずれたときの経済的損失をL(y)とおく.
損失関数L(y)を近似式で求めると
mが目標値であるから,一般性を失わないでL(m)=0とおける.また目標値になっているときの損失は最小で,目標値より大きくなっても小さくなっても,損失が増えるので,目標値mでの微分値L'(m)もゼロとおける.従って次の条件が成立する.
(10.1)
(10.2)
L(y)をmのまわりにテーラー展開する.
(10.3)
L(m)とL'(m)を代入すると,上式は次のようにかける
(10.4)
3次の項は矛盾があり,4次の項以上を省略して2次の項で近似すると
(10.5)
未知なる比例定数kを決めるには,機能限界と機能しなかったときの損失が必要である.
望目特性の場合を例に比例定数をもとめる.
機能限界を⊿0とおき,機能しなかった時の損失A0とおくと,前式の左辺にA0,右辺に⊿0を代入すると
(10.6)
(10.7)
が得られる.しからば損失関数Lは次式で与えられる.
(10.8)
多数の製品を作っている時や,特性値が変化するとき品質水準を評価しようとするならば,分散の平均値を使って次のように表す.
(10.9)
同様に望小特性の損失関数は
(10.10)
望大特性の損失関数は
(10.11)
となる.
すなわち,損失を最小にするためには,3種類の変数を調整する方法がある.
この様な関数を使うことによって,システム選択をしようとしたときの機能性のレベルと,システムのコストを合算することで,最終的な比較が出来る.但し,安全設計を導入することにより機能しなかったときの損失が大きく変わることになるので,フェールセーフの安全設計は非常に重要となる.これも,安全設計を入れた場合の損失金額は安全装置のコストとばらつきによる損失を合計したものであり,安全設計を入れない場合の損失金額との比較をしてコストの安い方法を選択すればよいのである.
11.許容差設計
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
3種の材料A1,A2,A3の寸法温度係数b(1℃当たりの伸びパーセント)と,1年当たりの摩耗量β(1年当たりの摩耗量パーセント)を調べたら下表の通りだった.
この寸法が,Δ0=6%変化すると市場でトラブルが発生し,その時の損失A0は18000円である.A1,A2,A3の中で最適な物はどれか.ただし,その材料が使用される温度条件xの標準偏差σxは15℃,設計寿命は20年である.
b(%)β(%)価格(円)
A10.080.15180
A20.030.06350
A30.010.05630
標準温度で出荷時の寸法は目標値mに等しいように生産されるから,温度のばらつきと劣化によるばらつきの合計の分散は次式で表される.
(11.1)
上式の後の項は次の様に求められる.年当たりの摩耗量をβとして,設計寿命をT年とした時の分散は次のようになる.
(11.2)
11.2式にσx=15(℃),T=20(年)を代入して,A1,A2,A3の材料の分散は
(11.3)
(11.4)
(11.5)
b(%)β(%)価格(円)σ2品質水準L総損失
A10.080.151804.4422202400
A20.030.063500.6825341691
A30.010.056300.3558178808
従って,最適解はA2の材料である.
12.生産工程の許容差設計
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
生産工程における日常の管理では,目的特性をコントロールするのに,原因ではなく調整因子を用いて修正をする方式,いわゆるフィードバック制御が用いられている.生産工程では製品品質に対する許容差Δが与えられている.
生産工程では許容差Δを割った製品が出来たとき,工程機能がだめになったと考えられる.その値Δを生産工程の機能限界とするのが妥当である.従って,製品のスペックの許容差Δを機能限界として損失関数を求める.規格を割った物や不合格品が出来たときの生産部門の損失(廃棄や手直し)をA円として,損失関数は次式で与えられる事になる.
(12.1)
(12.2)
(12.3)
これらの式は製品を1個しか作らない場合の損失である.しかし一般の生産工程では,多数の製品を作るので,各値に対する損失の平均,いわゆる品質水準を目的特性の理想値からのずれの2乗の平均σ2でおきかえ,次式で求める.
(12.4)
(12.5)
ただし,n個のデータy1,y2,・・・yn が求められているときσ2は次式で定義される.
(12.6)
(12.7)
(12.8)
13.許容差の決め方
(引用:田口玄一,開発・設計段階の品質工学,日本規格協会,1988)
安全係数は今までも求められてきた.多くの場合,4~5が米国でも一部の日本の会社でも用いられているようである.各分野で用いられている安全係数は経験的に決定されている場合が多く,論理的な説明ができないことが多い.
品質工学では安全係数φを次式で求めることを提案して,海外でも使われ始めている.
(13.1)
これを代入すると
(13.2)
証明すると
(13.3)
の(y-m)は目標値からの偏差であり,その許容のレベルを許容差Δ,Aは許容差設計で品質とコストのバランス点として求めた値であるとすれば,式(13.3)より
(13.4)
(13.5)
但し, (13.5)
となる.ここで, を安全係数という.
工場での規格Δは次のようにして定まる.
望目,望小特性のとき (13.7)
望大特性のとき (13.8)
下位特性の許容差に関してもこの考え方を適用して定める.
14.実験計画法と直交表
(引用:田口玄一,品質設計のための実験計画法,日本規格協会,1988)
安定した性能を発揮するためには,最適なパラメータを選択しなければならない.しかしながら,そのパラメータの組み合わせは指数関数的に増加してしまう.たとえば,A,B,Cの3種類のパラメータを選定しなければならない場合,それぞれのパラメータに対して2水準の選択肢が有ったとする場合には,次のような組み合わせがある.
1.A1,B1,C1
2.A1,B1,C2
3.A1,B2,C1
4.A1,B2,C2
5.A2,B1,C1
6.A2,B1,C2
7.A2,B2,C1
8.A2,B2,C2
この8通りとなる.
三つの因子のあらゆる水準の組み合わせの設計条件について研究する場合,3元配置にするという.
しかし,安定性の良い条件を探すために取り上げられた制御因子の数が多い場合のわりつけでは,多元配置を採用することはなく,ほとんどの場合直交表を利用する.直交表を使ったわりつけでは,すべての組み合わせではなく,直交表で決められる特定の組み合わせ条件を対象にするのが特徴である.
直交表には2水準系,3水準系,混合系などがある.もっとも規模の小さい直交表がL4(23)で,次のような構成になっている.
番号↓・列→1列2列3列
No.1111
No.2122
No.3212
No.4221
番号は,実験番号またはわりつけ番号とよばれ,1から4まである.一方,縦の列は直交表の列と呼ばれ,どの列も,1と2という数字4個ずつから構成されている.従って,ある列と別の列の数字の組み合わせは,1と2の数字の組み合わせだから,4とおりということになる.
二つの列がいずれも1と2という数字を含んでいて,4通りの組み合わせ(11),(12),(21),(22)が同じ回数で現れている場合,その2列はバランスしているとか,直交しているなどといわれる.
Aを1列,Bを2列,Cを3列にわりつけたとすると,Cの変動は,L4のNo.1からNo.4の観測値をy1,y2,y3,y4,としたとき,Cがわりつけられている3列の第1水準の合計y1+y4,第2水準の合計y2+y3を求めた上で,
(14.1)
とした.
ところで上式の(y1+y4)-(y2+y3)の部分は
(14.2)
と書くことができる.ここでC以外の条件に着目すると,y1はA1B1,y2はA1B2,y3はA2B1,y4はA2B2であるから,
(14.3)
となる.これは
Aが第1水準の下でのBの差-Aが第2水準の下でのBの差
で,Aの水準によるBの効果の差を表している.これをAとBの交互作用という.つまりCの変動として計算したものが,実はAとBの交互作用の変動を計算したことにもなっている.この様になることを主効果Cと交互作用A×Bとが交絡するという.
観測値のもっとも良くなる条件を最適条件という.直交表は少ない実験回数で最適条件を推定することにある.しかしながら,最適条件がいつでも直交表にある組み合わせであるとは限らない.
A1B2C2における推定値をμとすると,
μ=全体の平均+A1によって良くなる効果
+B2によって良くなる効果
+C2によって良くなる効果
であると考えられる.ただ,このようにすべての効果を加えることは過大評価になるので,実現する値を推定するには,大きな効果だけを考えるのが良いとされている.たとえば,C2の効果がもっとも大きかった場合は,
μ=全体の平均+C2によって良くなる効果
である.
全体の平均を とすれば, によって良くなる効果は
(14.4)
で表される.
(14.5)
この様に推定される.
直交表には,2列間の交互作用が特定の列の効果と交絡するタイプのものと,そうでないものとがある.一般に2n系(L4,L8,L16など),3n系(L9,L27など)と言われているものは前者で,混合系直交表は後者である.
L12,L18,L36は混合系直交表で,2列間の交互作用が特定の列の効果と交絡しない.したがって,仮に交互作用があってもいろいろな列に現れるから,各列の効果は,そこにわりつけられた因子の主効果の他に,いろいろな列の交互作用が何割かずつ上乗せされる.従って,本来大きい主効果を持つ因子のわりつけられている列の効果は,そうでない列の効果に比べて相対的に大きくなるから,本当に大きい因子の選択が可能になる.
直交表の内側には主として制御因子を割り付ける.2水準系の因子が多い場合は2水準系の直交表を,3水準の因子が多い場合は3水準系を使うことが便利なのだが,前述の理由から混合系を使うことが望ましい.その中でもL18は2水準と3水準の両方の因子を取り扱える上,規模が大きすぎないのでもっとも使いやすい直交表である.
しかし,割り付ける要因の数が直交表の列の数とぴったり一致しなかったり,水準の数が多すぎたり,足らない場合も発生する.その様な場合は,ダミー法 組合せ法,多水準作成法などの手法を使って対処する.ダミー法は2水準を3水準の列にわりつける場合に適用する.特に重要な水準を重複してわりつけて
B1=B1 B2=B2 B3=B1
のようにする.
組合せ法は2水準系の要因2つを3水準系の1列にわりつける場合に適用する.
(AB)1=A1B1
(AB)2=A2B1
(AB)3=A1B2
このようにする.(AB)1と(AB)2でA1とA2の差が算出できる.また(AB)1と(AB)3でB1とB2の差が算出できる.
多水準作成法は混合系の場合L18(21×37)の1列目と2列目に例外的に使える方法で
(11)1=A1
(12)2=A2
(13)3=A3
(21)4=A4
(22)5=A5
(23)6=A6
のようにわりつけられる.
2水準のAと5水準のBを組み合わせれば
(AB)1=A1B1
(AB)2=A2B1
(AB)3=A1B2
(AB)4=A1B3
(AB)5=A1B4
(AB)6=A1B5
としたり,
3水準のA,2水準のB,3水準のCを
(ABC)1=A1B1C1
(ABC)2=A2B1C1
(ABC)3=A3B1C1
(ABC)4=A1B2C1
(ABC)5=A1B1C2
(ABC)6=A1B1C3
のようにわりつけることもできる.
このような組合せ実験を実施した場合に困ることは,欠測値が有った場合である.余裕があれば,実験をやり直してデータをとることによってそのようなことは発生しないが,実験に失敗して材料が無くなってしまったり,資金が無くなってしまったりして再度データをとることが不可能な場合などは,逐次近似という方法を使う.採取できなかったデータには,直交実験全体の中でもっとも悪いデータかその2倍から3倍悪いデータを当てはめてみて,全体の分析推定をしてみる.その結果から,データを採取できなかった組合せの値を推定して,そのデータを当てはめてみる.これを繰り返して,推定の精度を上げていくわけである.
実験結果の解析の手順をL18の直交表を例に説明すると次のようになる.
直交表L18による実験結果が次のように得られたとする.
No.ABCDEFGH結果
111111111Y1
211222222Y2
311333333Y3
412112233Y4
412223311Y5
612331122Y6
713121323Y7
813232131Y8
913313212Y9
1021133221Y10
1121211332Y11
1221322113Y12
1322123132Y13
1422231213Y14
1522312321Y15
1623132312Y16
1623213123Y17
1823321231Y18
これらから総括表を作成する.
計測値
水準1水準2水準3
A(Y1+Y2+…+Y9)/9(Y10+Y11+…+Y18)/9
B(Y1+Y2+Y3+Y10+Y11+Y12)/6(Y4+Y5+Y6+Y13+Y14+Y15)/6(Y7+Y8+Y9+Y16+Y17+Y18)/6
C(Y1+Y4+Y7+Y10+Y13+Y16)/6(Y2+Y5+Y8+Y11+Y14+Y17)/6(Y3+Y6+Y9+Y12+Y15+Y18)/6
D(Y1+Y4+Y9+Y11+Y15+Y17)/6(Y2+Y5+Y7+Y12+Y13+Y18)/6(Y3+Y6+Y8+Y10+Y14+Y16)/6
E(Y1+Y6+Y7+Y11+Y14+Y18)/6(Y2+Y4+Y8+Y12+Y15+Y16)/6(Y3+Y5+Y9+Y10+Y13+Y17)/6
F(Y1+Y6+Y8+Y12+Y13+Y17)/6(Y2+Y4+Y9+Y10+Y14+Y18)/6(Y3+Y5+Y7+Y11+Y15+Y16)/6
G(Y1+Y5+Y9+Y12+Y14+Y16)/6(Y2+Y6+Y7+Y10+Y15+Y17)/6(Y3+Y4+Y8+Y11+Y13+Y18)/6
H(Y1+Y5+Y8+Y10+Y15+Y18)/6(Y2+Y6+Y9+Y11+Y13+Y16)/6(Y3+Y4+Y7+Y12+Y14+Y17)/6
T(Y1+Y2+…+Y18)/18
総括表から要因効果図を作成して判断するのである.それぞれの効果の差が大きければ,勾配が急になるので,まず第1の判断基準となる.実験の要因の取り方と水準の設定がうまくいけば,あるいっていの勾配の折れ線グラフが現れる.山になったり谷になったりするのは,交互作用が強く働いているなどの要素が考えられ,再び実験をしても再現性が無い場合が多い.従って,最適パラメータを選定する場合などは,その分割り引いて考えなければならない.
水準を選んだ効果の合計値を選んで,最終的な効果を推定する.たとえば,上記の様な要因効果図が得られたとすると,最適パラメータは次の通りである.
A2,B1,C1,D1,E1,F3,G2,H3である.
このパラメータを選択したときの推定値は,
しかし,この推定値は良すぎる.パラメータの選択はコストや制約条件が無いかぎりは全部を選択することが好ましいが,効果を予測する場合には,半分くらいのパラメータの効果で推定した方が現実に合うことが多い.
L12(211)
列番 1 2 3 4 5 6 7 8 91011
No.111111111111
No.211111222222
No.311222111222
No.412122122112
No.512212212121
No.612221221211
No.721221122121
No.821212221112
No.921122212211
No.1022211112212
No.1122121211122
No.1222112121221
L18(21×37)
列番 1 2 3 4 5 6 7 8
No.111111111
No.211222222
No.311333333
No.412112233
No.512223311
No.612331122
No.713121323
No.813232131
No.913313212
No.1021133221
No.1121211332
No.1221322113
No.1322123132
No.1422231213
No.1522312321
No.1623132312
No.1723213123
No.1823321231
15.基本機能の考え方
設計業務は,製品に対して自然現象を人工的に利用するということである.すなわち,その製品に対しては,設計者はその創造主となる訳である.したがって設計者の意図無しにその自然現象が起きるわけではなく,設計者の設計図通りに作られたシステムで,自然現象が発生しているだけである.自然現象は,すなわちエネルギーの変換でもある.
家電製品の多くは,電気エネルギーをもとにエネルギー変換が行われている.たとえば扇風機では,まずモーターを介して運動エネルギーに変換したりしている.その運動エネルギーを送風のエネルギーに変換したりしているのである.そのときのエネルギー変換効率のロスが,様々な弊害項目として現れるのである.電気エネルギーからモーターにて回転エネルギーに変換する過程では,熱エネルギーや電波ノイズなどによって拡散するものがある.回転エネルギーから送風エネルギーに変換する段階では,振動エネルギーや,騒音などになって拡散するものがある.モーターの設計者はさらにモーター内部の細分化されたエネルギー変換に関して設計をしている.
設計者の意図では,高い効率で目的のエネルギーに変換したいのであるが,現実には,全部が目的エネルギーに変換されることはなく,エネルギーの一部が意図していないエネルギーに変換されてしまうのである.
またその製品の善し悪しは,顧客ニーズにあっているかどうかにも依るが,顧客ニーズに合っているかどうか関しては,商品企画の機能を持っている部署の責任である.顧客ニーズに合っているかどうかは品種の問題である.
一方,設計者の役割は,製品に利用した自然現象のエネルギー変換の効率をより高くすることにある.エネルギー変換の効率が悪くなると,様々な弊害項目が発生することになる.そのため,早期からエネルギーの変換に注目して,これを評価する測度を持つ必要がある.
(引用:機能性評価による機械設計,上野憲造,日本規格協会1995)
自動車のブレーキの役割は,走行している自動車を減速させたり,あるいは停止させるために,自動車が走行時に持っている運動エネルギーを,摩擦材によって熱エネルギーに変換し,自動車の運動エネルギーを減少させることである.同時に蓄積した熱エネルギーを大気中に放出して,ブレーキとしてのエネルギー変換機能を維持しておかなければならない.この様にシステムに要求される役割のことを目的機能と呼んでいる.
システムが選択された後,選択されたシステムのばらつきが小さく,安定して機能するようにパラメータ設計を行う.そのためには目的機能を確実に達成させるための技術的な手段やメカニズムを検討する.ここで明らかになった技術的手段やメカニズムのことを基本機能と呼んでいる.基本機能すなわち正しい入出力関係を明らかにすることができれば,パラメータ設計は成功したも同然である.
通常の足踏み式ブレーキは,ブレーキを踏むと踏力が発生し,踏力に応じて制動力が発生するような仕組みになっている.さらに細分化すると,まずブレーキペダルを踏んだ踏力によって油圧を発生させ,発生させた油圧を伝達させて制動トルクを発生させている.つまり,入力はいろいろな大きさの油圧であり,出力はそれぞれの油圧の大きさに対応する制動トルクである.したがって,基本機能はいろいろな大きさの油圧と,各々の油圧の大きさに対応した制動トルクの間に比例関係の直線が成立することである.
ある速度で自動車が走行している時に,これを停止させるために必要な制動力(制動トルクに相当)をF0とする.ブレーキAのばあいは踏力PAによりF0を発生するが,効率100%の理想的なブレーキで得られるはずの制動力FAとの差が,余剰エネルギーとして消費され鳴きや振動という現象になって現れてくるのである.一方ブレーキBのように設計による改善を図り,エネルギー変換効率を向上させたブレーキでは,制動力F0を得る踏力をPBまで低減することができる.
16.特性値の種類とSN比
システムの安定度を評価するときに,品質工学ではSN比を使うことを主張している.もともとは,通信の世界で信号とノイズの比として使われてきたが,パラメータ実験の時の,入力信号に対する出力の変化を評価する分野に拡張したものである.前述の様に特性値には4種類あるので,それぞれにSN比の計算式は異なる.
16.1望小特性のパラメータ設計
望小特性では非負でゼロが望ましい特性を望小特性という.摩耗量,不純物の量,排ガス中の有害成分などが望小特性である.
望小特性は,いろいろなノイズの条件でデータを取り,それをy1,y2,・・・,ynとし,目標値ゼロからの差の2乗の平均を分散として,平均値の変動と誤差変動を総合評価する次のSN比ηを評価特性とすべきである.
(16.1)
だだしσ2は分散で
(16.2)
である.yiの平均値をm,標準偏差をsとすれば,σ2の期待値E(σ2)は
(16.3)
16.2望大特性のパラメータ設計
次のSN比ηを評価特性とすべきである.
(16.4)
だだしσ2は分散で
(16.5)
16.3望目特性のパラメータ設計
望目特性の場合,安定性の測度になるのは平均値mと標準偏差σの比である.
その比の2乗をSN比ηという
(16.6)
誤差率σ/mの2乗の逆数が安定性の測度SN比である.
ところで,m2とσ2をどうして推定するかである.y1,y2,・・・,ynというn個のデータがある時,平均値mと分散のσ2は
(16.7)
(16.8)
で推定される.
二つのデータしかない例でも
(16.9)
で分散σ2を推定する.一方で平均値
(16.10)
には誤差があるので(y)2でm2を推定するのは平均として過大になる.n個のデータの場合は,
(16.11)
としたときにその期待値はよく知られるように
(16.12)
である.従って,m2の推定値としては
(16.13)
のほうが望ましいことになる.上式のmは感度の大きさと呼ばれている.
従ってSN比ηと感度の大きさであるSは次式で推定する.
(16.14)
(16.15)
ここに
(16.16)
(16.17)
とくにデータが2個の場合は
(16.18)
(16.19)
である.制御因子の効果を解析するには,式(9.18)と(9.19)の常用対数の10倍であるデシベル値を用いる.
(16.20)
(16.21)
16.4動特性のSN比
動特性は入力と出力の関係から通常次の4種類に分類される.
場合入力出力
①計量値計量値
②計量値ディジタル
③ディジタル計量値
④ディジタルディジタル
入力に応じて出力を変えたいのだが,出力は入力のみでなく,様々なノイズ(誤差原因)によって影響を受ける.たとえば計測器の場合は入力である信号因子と直線関係に有れば2つの標準で校正可能だから入力をMとしたとき
(16.22)
が理想関係となる.時計やヘルスメータの場合,ゼロ点校正は消費者によって行うことができるので,多くの動特性と同様に,ゼロ点校正後のみを考えて次の比例関係
(16.23)
を理想関係とすることができる.いま,信号因子と誤差因子でnとおりの組み合わせで実験や解析計算をし,n個のデータが得られたとする.それをy1,y2,・・・,ynとする.いまそれらがゼロ点校正後のデータとして,全2乗和
(16.24)
で全出力の大きさを求める.次に信号因子はk水準としてM1,M2,・・・Mkでそれぞれr1,r2,・・・rk個のデータが得られた物としよう.もちろん
(16.25)
が成立している.M1,M2,・・・Mkに対するr1個,r2個,・・・rk個のデータの和をY1,Y2,・・・Ykとして次のSβをもとめる.Sβは信号の比例項の変動または(回帰変動)である.
(16.26)
このSβは,信号因子の影響の大きさと誤差分散σ2の和である次の値
(16.27)
を推定している.いまβ2の係数をrとすれば
(16.28)
である.rは信号因子の全入力の変動で,それは有効除数と呼ばれている.また,σ2は誤差分散である.したがって,誤差分散σ2の推定値をVeとしたとき
(16.29)
は,β2を推定していることになる.この式を感度の大きさというが,感度に対する制御因子の効果を求めたい時には,次の感度のデシベル値
(16.30)
を解析することになる.
一方,誤差分散σ2は次のように推定する.全出力であるSTから信号の効果を引いて誤差変動Seを求める.
(16.31)
これを自由度(n-1)で割って,誤差分散σ2の推定値Veをもとめる.
(16.32)
動特性のSN比ηは次式で推定する.
(16.33)
(16.34)
制御因子の効果を求めるときには,デシベル単位のSN比として
(16.35)
を計算する.
ここで算出された標準偏差が,前出の損失関数として使えるわけである.損失関数で比較することによって,製品の品質(機能性)と価格のバランスを保つことができるのである.
16.5誤差因子を調合した場合の動特性のSN比
信号因子をk水準にとりN1,N2,N3の誤差因子とMの組合せで出力を求めた場合は,次のように計算する.
M1M2・・・Mk線型式
N1y11y12・・・y1kL1
N2y21y22・・・y2kL2
N3y31y32・・・y3kL3
計y1y2・・・yk
全変動: (f=3k) (16.36)
回帰変動: (f=1) (16.37)
Nの主効果:
(f=2) (16.38)
誤差分散
誤差変動: (16.39)
また比例定数をβとして,β2の推定値は
(16.40)
(16.41)
しかしながらSN比を求めるときの誤差分散はVeではなく,Nの効果を含めた
(16.42)
を用いなければならない.
(16.43)
デシベル値の場合は
(16.44)
VeのかわりにVNを用いる理由は,比例定数βが誤差因子の条件で変化するのは誤差であり,それをゼロにしたいからである.
誤差因子を調合して2水準にすると,SβとSN×βは更に簡単になり,次のようになる.
(16.45)
(16.46)
17.品質工学を活用した技術開発の手順
17.1 基本機能の定義
動特性の場合は、設計開発するシステムに採用しようとしている入力と出力の関係を定義する。品質工学では、基本機能の定義と言い、最も重要な段階となる。基本的にエネルギー変換のシステムを開発するのであるから、入力エネルギーとして何を選択するか、実現したい出力エネルギーを何にするかを決定する。最も根本となる物理現象や化学反応から入力と出力の具体的な物理量を定義することになる。このとき入力エネルギーとして定義したものが信号因子となり、出力と定義したものが計測する特性値になる。品質工学では、入力エネルギーと出力エネルギーの変換は直線関係にあるとしているが、計測できる特性値がそのままエネルギー量と比例していない場合もあるため、計測値に置き換える場合は、標準SN比などで定義する。
静特性の場合は、目的機能をそのまま計測することになるので、基本機能の定義は行わない。しかし、静特性として捉えられている特性値でも、将来のスケールアップ等が考えられる場合は動特性として考えてみることも有効である。
17.2 要因と水準の決定
基本機能の定義が決定されたなら、入力と出力の関係に影響を及ぼす要因とその水準を決定する。要因としては、制御因子と誤差因子の2種類が検討される。
L18直交表の場合、内側に8つの要因を割り付けられる。どれだけ有効な要因を思いつくかが固有技術となる。ここで選択した組み合わせの中で最適パラメータの選定が行われるため、固有技術の無い人は、品質工学を使っても優位性のあるパラメータの組み合わせを見つけることは出来ない。また水準の数や、水準の幅についても、なるべく大きな値から絞り込んでゆく。
要因については、異なるシステムのパラメータを混合しないようにする。異なるシステムの場合は、異なる直交表に割り付けることになる。
システム使用上の外乱として考えられる誤差因子も同時に検討する。ユーザーの使用条件などを検討して要因と水準を決定する。ユーザーの使用範囲の限界などを設定する。
17.3 直交表への割り付け(内側と外側)
要因と水準が決定されたところで、直交表への割り付けを行う。L18直交表に割り付けることになる。要因の数が多くなりもっと大きな直交表を使いたくなる場合も有ると思うが、なるべくコンパクトな実験にして、PDCAのサイクルを早く回した方が結果的に早く最適パラメータにたどり着く。そこで、有望なパラメータでいったんL18の直交表で実験を行い、特性要因図から特性値に効果の低い因子と、初回割り付けできなかった因子を交替させてL18実験を繰り返すことである。
制御因子は直交表の内側に割り付け、誤差因子は直交表の外側に割り付ける。
17.4 実験の実施
直交実験では、なるべく実験の順序をランダマイズさせて実施することが好ましい。実験の順序で劣化したり習熟することで結果に影響を与えたりすることで実験結果の誤差が主効果に混ざることを排除するためである。実験の途中で欠測値が多発した場合は、要因の水準を見直したりして実験をやり直すなどの判断が必要である。
17.5 データの解析
得られたデータからSN比と感度を計算して要因と水準毎の平均値を集計した総括表を作成し、要因効果図を作成する。
17.6 最適パラメータの決定(効果の推定)
SN比と感度の要因効果図を見ながら、SN比の高いモノから最適パラメータを選定する。往々にしてSN比の高いパラメータは感度が低くなることも少なくない。その場合は、SN比をあまり低下させずに感度を向上させるパラメータを選択して調整する。
最適パラメータの選定が決定された後に選定したパラメータの組み合わせでのSN比を推定しておく。このとき、取り上げたパラメータのSN比及び感度で上位から約半数の工程平均を使って推定する。
17.7 効果の確認(再現性の判定)
選定された最適パラメータの組み合わせで確認実験を行う。実験に依って得られた結果について、SN比と感度を求める。確認実験によって得られたSN比と感度と推定によって得られたSN比と感度を比較して再現性を確認する。その差が3デシベル以下の場合は再現していると判断できる。それ以上の場合は実験誤差が大きく再現していないという判断になる。
結果が目標値に達していれば、最適化が完了しているが、目標値に達していない場合や、再現していない場合は、要因そのものを入れ替えて実験するか、要因の水準を見直して再度直交実験を行う。この場合、今回取り上げた要因と水準の中に最適パラメータの組み合わせが無いと言うことを示している。
18.生産システムにおける適用
18.1品質特性によるフィードバック制御
(引用:田口玄一,製造段階の品質工学,日本規格協会,1989)
次のようにパラメータを定義する
目標特性の規格値:
不良品損失:A(円)
計測コスト:B(円)
調整コスト:C(円)
現行の計測間隔:n0(個)
現行の平均調整間隔の観測値:u0(個)
現行の調整(管理)限界:D0
計測方法のタイムラグ:l(個)
最適計測間隔:n(個)
最適調整限界:D
平均調整間隔の予測値:u(個)
この時の最適計測間隔nは
(17.1)
また最適調整限界Dは
(17.2)
最適システムの損失関数は
(17.3)
現行条件の場合は
(17.4)
18.2 経済的点検・保全間隔の算出方法
設備総合効率を向上させるためには,設備に対する保全活動を十分に行えばよいのである.しかしながら,社内で行う保守点検活動も無料で行えるわけではないので,経済性を考えなければならない.一回の点検・整備に関わる作業が非常に高いコストがかかる場合は,なるべく間隔を長くとりたいし,故障することによって作られる不良品を廃棄するためのコストが非常に高いのであれば間隔を短くとりたい.自ずと,それらのバランスをとったところで,経済的な点検間隔が存在するはずである.そこで品質工学の考え方を導入して,設備の点検間隔の算出を行い,経済的な点検間隔で点検を行う必要がある.以下にいくつかの経済的点検間隔の算出方法に関しての公式を紹介する.以下の式に代入して算出をしてみると,論理的に点検間隔nと保全限界Dを設定することができる.ここで示してある公式は3種類ある.最初の公式は定期点検を行いながら定期保全を併用してゆく場合である.2番目の公式は,定期保全のみ行っている場合である.3番目の公式は定期保全を行っている場合である.式内のLは現在の品質水準を表現するための損失関数である.
予防保全方式の設計(定期保全と定期点検の併用の場合)
(17.5)
ただし
ただし
予防保全方式(定期点検の場合)
定期保全(定期交換の場合)
参考文献
「開発・設計段階の品質工学」 田口玄一 刊行委員会委員長 日本規格協会 1988
「製造段階の品質工学」 田口玄一 刊行委員会委員長 日本規格協会 1989
「品質設計のための実験計画法」田口玄一 刊行委員会委員長 日本規格協会 1988
「機能性評価による機械設計」上野憲造 日本規格協会 1995